【算法导论】二叉树的建立

基本概念：

​ 有序树与无序树：若将树中的每个节点的各个子树都看成是从左到右有次序的，则称该树为有序树，否则为无序数。

​ 顺序存储：从根节点起，自上而下，从左至右的方式对节点进行顺序编号，编号即对应为要存储的数组的下标。于是节点与数组元素就一一对应了。

​ 满二叉树、完全二叉树、非完全二叉树的区别：

​

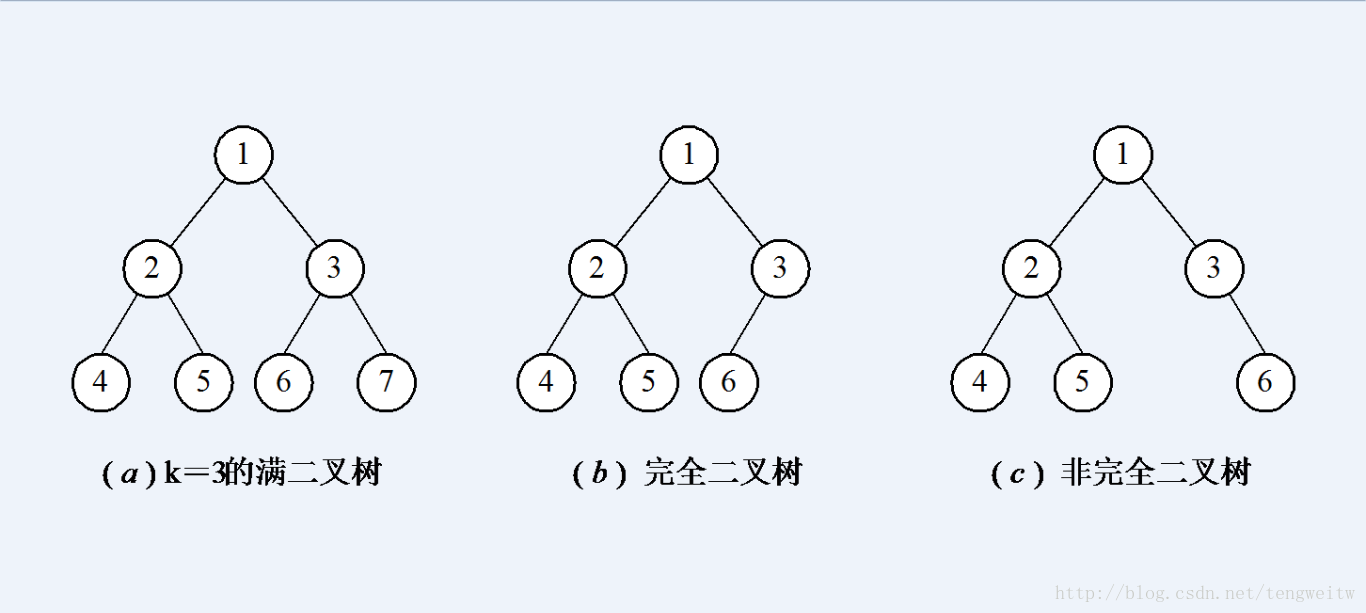
二叉树的性质：

• 性质1 在二叉树的第i层上至多有$2i-1$个结点($i≥1$)
• 性质2 深度为k的二叉树至多有$2k－1$个结点($k≥1$)
• 性质3 对任何一棵二叉树，如果其终端结点数为$n_0$，度为2的结点数为$n_2$，则$n_0=n_2+1$
• 性质4 具有n个结点的完全二叉树的深度为$\lceil \log_2n\rceil+1$或$\lfloor\log_2(n+1)\rfloor$。

二叉树建立的基本思想：依次从原数组中读取结点信息，建立一个新结点来存储这个元素信息。若新结点是第一个结点，则令其为根结点，否则将新结点作为孩子链接到它的双亲结点上。如此反复进行，直到数组元素全部读完为止。为了使新结点能够与双亲结点正确相连，并考虑到这种方法中先建立的结点其孩子结点也一定先建立的特点，可以设置一个指针类型的数组构成的队列来保存已输入结点的地址，并使队尾(rear)指向当前输入的结点，队头(front)指向这个结点的双亲结点。由于根结点的地址放在队列的第一个单元里，所以当rear为偶数时（注意根节点不是数组的第一个元素），则rear所指的结点应作为左孩子与其双亲链接，否则rear所指的结点应作为右孩子与其双亲链接。若一个双亲结点与两个孩子链接完毕，则进行出队操作，使队头指针指向下一个待链接的双亲结点。

具体算法如下：

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>

#define maxsize 10
typedef int datatype;
typedef struct node
{
	datatype data;
	struct node *lchild,*rchild;
} bitree;//二叉树的节点结构

bitree* CreatBitree(int* arrayA,int n);//创建二叉树（以顺序存储方式）
void preorder(bitree *p);//先序遍历算法
void midorder(bitree *p);//中序遍历算法
void postorder(bitree *p);//后序遍历算法

void main()
{
	int arrayA[9]={0,1,2,3,4,5,6,7,8};//第一个节点没有用于存储数据，是为了方便计算
	int n=sizeof(arrayA)/sizeof(int);

	bitree *head=NULL;//初始化指向链表的头指针

	head=CreatBitree(arrayA,n);//建立链表

}

bitree* CreatBitree(int* arrayA,int n)//顺序存储 建立二叉树
{
	bitree *root;
	bitree *queue[maxsize];//队列用于保存已输入节点的地址
	bitree *p;
	int front,rear;
	front=1;rear=0;//指向队列的头尾
	root=NULL;

	for(int i=1;i<n;i++)
	{
		p=(bitree*)malloc(sizeof(bitree));//创立节点并赋值
		p->data=arrayA[i];
		p->lchild=NULL;
		p->rchild=NULL;

		rear++;
		queue[rear]=p;

		if(rear==1)//判断是否为输入的第一个节点
			root=p;
		else
		{
			if(i%2==0)//新节点为左孩子
				queue[front]->lchild=p;
			else//新节点为右孩子
			{
				queue[front]->rchild=p;
				front=front+1;
			}
		}

	}

	return root;
}